 |
|
숫자 2,147,483,647. 권오성 기자 sage5th@hani.co.kr
|
권오성의 세상을 바꾼 데이터
메르센 소수면서 32비트 정수형 최대치
2의 31승 빼기 1
이 숫자가 ‘강남스타일’과
‘2038년 문제’에 얽힌 비밀은?
 |
|
숫자 2,147,483,647. 권오성 기자 sage5th@hani.co.kr
|
2,147,483,647.
20억이 넘는 그저 크고 복잡하게 보이는 하나의 숫자다. 그러나 2,147,483,647은 아무 무작위의 수가 아니다. 숫자로서 신비한 성질과 데이터로서 함정을 동시에 지닌 특별한 숫자다.
2,147,483,647은 상당히 큰 수임에도 불구하고 소수다. 소수란 1과 자기 자신으로밖에 나눌 수 없는 정수를 말한다. 2, 3, 5, 7 등이 소수에 해당한다. 2,147,483,647은 소수 가운데에도 특별한 ‘메르센 소수’의 하나다. 메르센 소수란 소수 가운데 ‘2의 n승 빼기 1’로 표현되는 소수를 말한다.
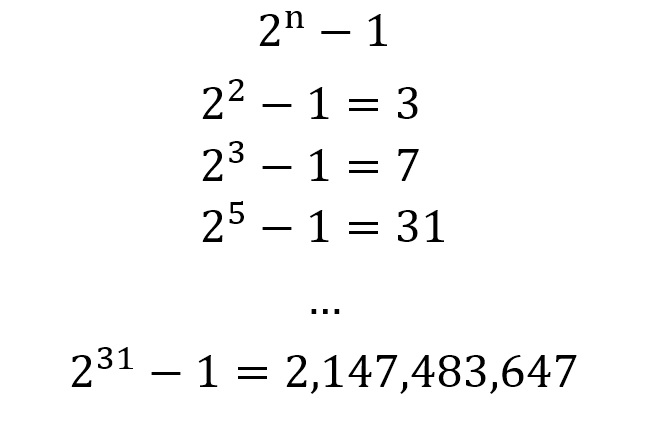 |
|
메르센 소수. 권오성 기자 sage5th@hani.co.kr
|
‘메르센’이란 이름은 이런 소수를 연구한 17세기 프랑스의 수학자 마랭 메르센에서 왔다. 예를 들어 3은 ‘2의 2승 빼기 1’인 메르센 소수다. 메르센 소수는 차례대로 3, 7, 31, 127, … 이렇게 나아간다. 2,147,483,647은 ‘2의 31승 빼기 1’로서, 역시 1과 자기 자신으로밖에 나눠지지 않는 소수다.
이런 형태의 숫자가 소수가 되기 위해선 n은 반드시 소수여야 한다. n이 소수가 아닐 경우 ‘2의 n승 빼기 1’도 소수가 아님은 수학적으로 증명되기 때문이다. 그래서 메르센 소수의 n은 모두 소수다. 그런데 n이 소수라고 해서 ‘2의 n승 빼기 1’이 반드시 소수가 되는 것은 아니다. 예를 들어 ‘2의 11승 빼기 1’은 2047인데, 23 × 89로 분해되어 소수가 아니다.
가장 큰 메르센 소수가 무엇인지는 세계 수학 애호가들의 관심사 중에 하나이다. 이를 찾는 국제 모임마저 있을 정도다. ‘위대한 인터넷 메르센 소수 탐색’(GIMPS·Great Internet Mersenne Prime Search)이 그런 그룹이다. 이들은 디지털 소프트웨어를 이용해 과연 어디까지가 메르센 소수인지 지금도 계산하고 있다. 지금까지 밝혀진 가장 큰 메르센 소수는 지난해 12월 GIMPS가 찾아낸 ‘2의 82,589,933승 빼기 1’이다. 자릿수만 24,862,048개에 달하는 어마어마한 크기의 소수다. 이는 지금까지 밝혀진 모든 소수 가운데 7번째로 큰 소수이기도 하다. 그럼에도 불구하고 메르센 소수의 순서로 치면 단지 51번째에 불과하기도 하다.
메르센 소수 2,147,483,647는 컴퓨터 과학과 데이터 측면에서 특별한 의미를 갖는다. 왜냐하면 32비트 컴퓨터에서 하나의 데이터로 저장할 수 있는 정수의 최대값이 바로 2,147,483,647이기 때문이다. 잘 알려져 있듯이 컴퓨터는 결국 0과 1로 구성돼 있다. 이런 ‘0 또는 1’의 데이터 최소 단위를 비트라고 부른다. 32비트란 비트가 32개 있다는 뜻이다. 그런데 양과 음이 있는 정수를 표시하려면 32비트 가운데 한 비트는 비워두어야 한다. 그럼 31개 비트가 남는데, 숫자가 0부터 시작하므로 최대로 담을 수 있는 정수의 크기는 ‘2의 31승 빼기 1’, 즉 2,147,483,647이 되는 것이다.
 |
|
싸이(PSY)의 강남스타일 뮤직 비디오의 한 장면. 유튜브(Youtube) 갈무리
|
그런데 어떤 정수 데이터가 담을 수 있는 최대치, 2,147,483,647을 넘어가면 무슨 일이 벌어질까? 더 이상 계산이 안되거나, 0으로 돌아가거나, 분명 무슨 오작동이 일어날 것이다. 실제 이런 문제가 벌어진 적이 있는데, 우리나라 가수 싸이(PSY)의 세계적인 히트곡 ‘강남스타일’이 주인공이었다. 인터넷 동영상 플랫폼 유튜브는 처음 설계될 때 사용자 시청수를 32비트의 정수로 다루었다. 개발자들이 처음 만들 때만 해도 ‘설마 아무리 봐도 2,147,483,647회 이상 보는 영상이 있겠어?’ 생각했기 때문이다. 하지만 ‘강남스타일’이 그 설마를 깨뜨린 것이다. 유튜브 개발진은 2014년 강남스타일의 시청수 카운터가 2,147,483,647를 넘어가기 전에 32비트 정수에서 64비트 정수로 업그레이드 해야 했다.
1999년, 세계인들의 걱정을 샀던 문제 중에 ‘Y2K 문제’ 또는 ‘밀레니엄 버그’라고 불린 것이 있었다. 1960~70년대 컴퓨터 프로그래머들이 연도의 시작을 ‘19○○’으로 짰기 때문에 2000년이 시작되는 순간 수많은 컴퓨터들이 오작동을 하리라는 게 이 버그였다. 어떤 이들은 핵무기 관제 프로그램의 오작동으로 3차 세계대전이 일어날 수 있다다거나 금융 시스템이 붕괴할 것이라는 대담한 경고를 하기도 했다.
32비트 정수의 2,147,483,647 한계는 이와 유사한 ‘2038년 문제’를 예고하고 있기도 하다. 컴퓨터들은 보통 자체 타이머를 가지고 있는데, 32비트 컴퓨터의 경우 협정세계시(UTC)를 기준으로 1970년 1월1일 0시부터 1초 당 1씩 증가하는 정수형으로 이를 센다. 그런데 문제는 2038년 1월19일 새벽 3시14분7초가 되면 이 숫자가 정확히 2,147,483,647에 달하는 것이다. 3시14분8초에는 무슨 일이 벌어질까? 이번에도 컴퓨터의 오작동으로 핵미사일이 발사되는 일이 벌어지진 않을까? 다행히 많은 컴퓨터가 이미 64비트 시스템으로 전환했기 때문에 2038년에 그런 극적인 일이 벌어지진 않으리라는 게 다수 전문가들의 의견이다.
비록 지구 멸망을 몰고 올 오류는 아닐지라도 데이터를 보는 중에 2,147,483,647라는 숫자를 발견하면 한번쯤 의심해 보는 자세는 필요하다. 우연찮게 나온 숫자라고 하기에 2,147,483,647은 특별하기 때문이다. 컴퓨터 프로그램이나 데이터의 오류로 나온 숫자일 가능성이 높다는 뜻이다.
광고

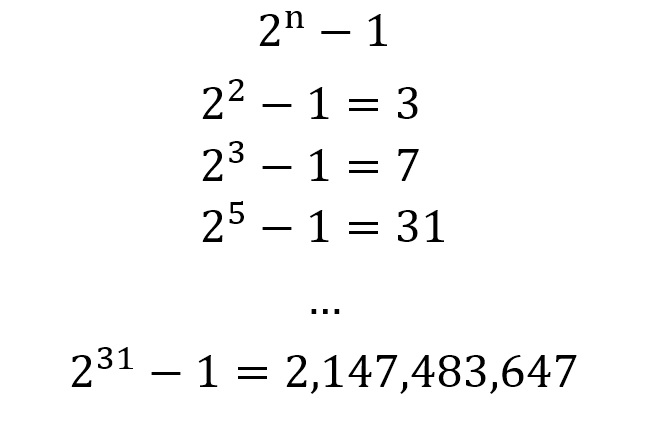



기사공유하기